Bisection Method of finding the roots of an equation is both simple and straight forward - I really enjoyed playing with bisection back in college (oooh yeah ES84 days) and I decided to make a post and implement bisection in scilab.
I also included a helper function that will plot the equation and will illustrate where the roots are by also plotting [latex] y = 0 [/latex] :)
First lets define bisection, here is what wikipedia has to say
But first! What is a root? Here's how algebra.com defines it:
When put into a graphe a root will look like this:
The numbers that correspond to a, b, and c above are the roots - it can also be observed that these are the values in which the line (function) crosses zero :) Bisection's root finding is then based on the principle that if there is a root between two points (it passes zero) then multiplying the result of the equation using those two points will result into a negative number!
Here is how bisection goes:
We now have our algorithm! Lets program! I would like you guys to program this by yourselves, in case your pressed for time you can get the code below to try it out. I also created a helper .sci file so that you can visualize the root and how many roots are there in that interval.
Lets program!
Featured image is from Code Project
I also included a helper function that will plot the equation and will illustrate where the roots are by also plotting [latex] y = 0 [/latex] :)
First lets define bisection, here is what wikipedia has to say
The bisection method in mathematics is a root-finding method which repeatedly bisects an interval and then selects a subinterval in which a root must lie for further processing.
But first! What is a root? Here's how algebra.com defines it:
I remember roots as the numbers you get when you equate a factor to zero and solve for x, (x-1) will result into a root of 1.A number is called a root of an equation if when the number is substituted into the equation and both sides simplified, the result is an identity, such as 2=2 or 8=8, etc.
When put into a graphe a root will look like this:
Source: codecogs
The numbers that correspond to a, b, and c above are the roots - it can also be observed that these are the values in which the line (function) crosses zero :) Bisection's root finding is then based on the principle that if there is a root between two points (it passes zero) then multiplying the result of the equation using those two points will result into a negative number!
Here is how bisection goes:
- There is a given equation and a range where we want to find the roots
- Evaluate the equation on both ends of the range - there must be a change of signs, if there is no change in signs then its either have no roots in the interval or you fell into a bisection pitfall. Note 1.
- If there is a change of sign then it means that there is atleast one root in the interval - lets iterate to find the root. Note 2.
- Get the center of the interval.[latex] center = \frac{upperLimit}{lowerLimi}[/latex]
- Check the two new sub-ranges, (lowerLimit,center) and (center,upperLimit), do step 2 on the two ranges, if the first subrange results into a change of sign then [latex] upperLimit = center[/latex]
- Evaluate the relative error of the result and if the error is with in bounds then [latex] root = center [/latex], if not then repeat step 4 (on the new interval) until error is met.
We now have our algorithm! Lets program! I would like you guys to program this by yourselves, in case your pressed for time you can get the code below to try it out. I also created a helper .sci file so that you can visualize the root and how many roots are there in that interval.
Lets program!
//The Bisectfunction will do bisection method in the expression 'theFunction'
// - using 'xLeft' and 'xRight' as the interval of interest
// - it will use the 'acceptableErrorInPercent' variable as the stopping criterion
//Note: xRight must be greater than xLeft for things to make sense
//PS. Please put us as a source when you use our code below :)
//This function will use plotThatThing which is declareed on a different .sci file please load it first
function [root]=MyOwnBisection(theFunction, xLeft, xRight, acceptableErrorInPercent)
//plot the function to get a look on how should it look
plotThatThing(theFunction, xLeft, xRight,0.001);
x = xRight;
fOfRight = evstr(theFunction); //Evaluate theFunction using the value at the right for the [xLeft,xRight] pair
x = xLeft;
fOfLeft = evstr(theFunction); //Evaluate theFunction using the value at the right for the [xLeft,xRight] pair
//Before trying to loop through the values, check first if there is a root in the interval
//- please take note that this check may fail when there are even number of roots in the given interval
if (fOfRight*fOfLeft >= 0) then
root = "There is no root between " + string(xLeft) + " and " + string(xRight) + "Or there might be an even number of roots in the said interval";
else
//There is a root! The number of roots can either be 1 or any odd number
exactSolution = 'not yet found';
howFarAreWeInPercent = 100; //Lets start with 100% away
midX =(xRight + xLeft)/2;
//Now lets start the loop - this will search for the root in the given interval
while howFarAreWeInPercent > acceptableErrorInPercent & exactSolution == 'not yet found',
x = midX;
fr = evstr(theFunction);
x = xLeft;
fOfLeft = evstr(theFunction);
//Choose the next subinterval to do bisection
if(fOfLeft*fr < 0) then
xRight = midX;
elseif(fOfLeft*fr > 0) then
xLeft = midX;
elseif(fOfLeft*fr == 0) then
root = midX;
exactSolution = 'found';
end
//Check for the darn error!
previousMidX = midX;
midX =(xRight + xLeft)/2;
howFarAreWeInPercent = abs((midX - previousMidX)/midX)*100;
end
//the current midX is assumed to be the nearest number to the target value
if (exactSolution == 'not yet found') then
root = midX;
end
end
endfunction
This function uses plotThatThing.sci which is the code below
//this will plot the given function/expression in the given interval
function plotThatThing(theFunction, xLeft, xRight, theStepSize)
x = xLeft : theStepSize : xRight;
y = evstr(theFunction);
plot(x, y, x, 0);
endfunction
Pitfalls of the bisection method:- It wont be able to detect roots if there is an even number of roots in the given interval this is Note 1.
- When the sign changes in a particular interval there could be more than 1 root, however bisection will only give you one.
- Im still thinking if you have more to add please leave a comment and ill add it to the list :)
Featured image is from Code Project



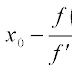



Hi there, can you please give an example with a function, how should be on the command line? [root]=MyOwnBisection(x^2+log(x), 0.5, 1, 10^-4)
ReplyDeleteis this a right way to call a function? I get "Undefined variable: x"!
Thanks.
Hi Sam,
ReplyDeleteYou will need to make sure that the functions (plotThatThing and MyOwnBisection) are loaded in scilab.
The command above is close you will just need to add quotes to the functions so it will end up like this:
--> root = MyOwnBisection('x^2+log(x)', 0.5, 1, 10^-4)
this is so because the MyOwnBisection function makes use of evstr which evaluates a string thus the first argument must be a string :)
cheers!
Hi,
ReplyDeleteI did load the functions beforehand.
I tried the line you said, now I get the following error:
"!--error 2 Invalid factor."
Can you explain please?
Thanks,
Hi Sam,
ReplyDeleteJust replace the single quotes with double quotes :)
-->root = MyOwnBisection("x^2+log(x)", 0.5, 1, 10^-4)
root =
0.6529183
Many thanks.
ReplyDeleteThanks for covering for me
ReplyDelete